Free Bonus: Big O Cheat Sheet 7 Time Complexity Classes on 1 Page Use this 1-page PDF cheat sheet as a reference to quickly look up the seven most important time complexity classes (with descriptions and examples). Big O notation cheat sheet. Big O notation is used to describe the complexity of an algorithm in terms of how well it scales. As a data set grows, so too can the number of cycles of processing timeand memory space requirements – this is known as scalability. Big O notation describes this effect, considering best-, worst- and average-case. Big O cheat sheets; intro; big O notation; data structures; algorithms; Github; About: I made this website as a fun project to help me understand better: algorithms, data structures and big O notation. And also to have some practice in: Java, JavaScript, CSS, HTML and Responsive Web Design (RWD). Big O notation cheat sheet provides the extended Big O notations for top interview questions. What is Big O notations? Big O notations describe the time or space required for the execution in software program. The execution can be an operation in data structures, such as add, delete or traverse. It can also be an algorithm, such as sort or search. Big O notation cheat sheet Big O notation is used to describe the complexity of an algorithm in terms of how well it scales. As a data set grows, so too can the number of.
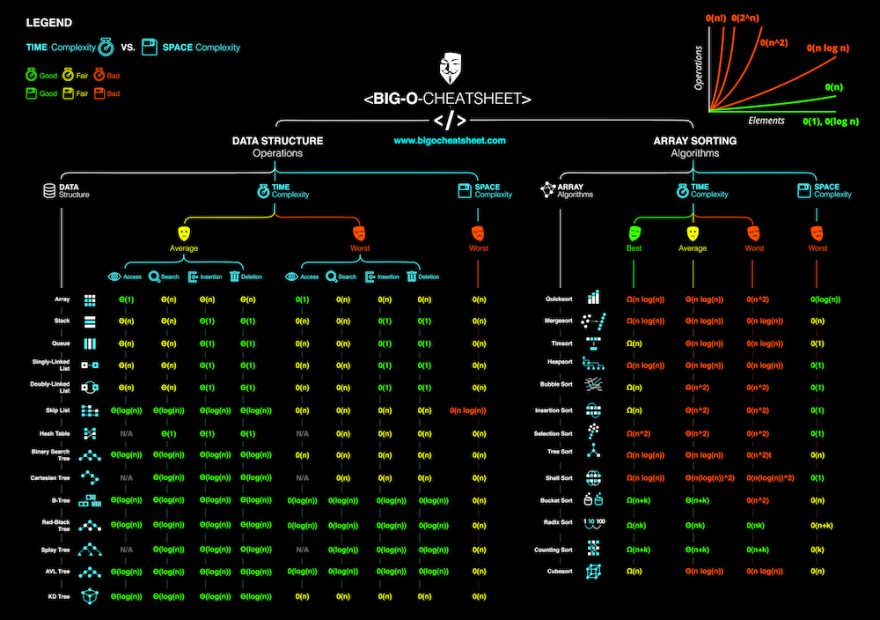
Sorting algorithms are a fundamental part of computer science. Being able to sort through a large data set quickly and efficiently is a problem you will be likely to encounter on nearly a daily basis.
Here are the main sorting algorithms:
| Algorithm | Data Structure | Time Complexity - Best | Time Complexity - Average | Time Complexity - Worst | Worst Case Auxiliary Space Complexity |
|---|---|---|---|---|---|
| Quicksort | Array | O(n log(n)) | O(n log(n)) | O(n^2) | O(n) |
| Merge Sort | Array | O(n log(n)) | O(n log(n)) | O(n log(n)) | O(n) |
| Heapsort | Array | O(n log(n)) | O(n log(n)) | O(n log(n)) | O(1) |
| Bubble Sort | Array | O(n) | O(n^2) | O(n^2) | O(1) |
| Insertion Sort | Array | O(n) | O(n^2) | O(n^2) | O(1) |
| Select Sort | Array | O(n^2) | O(n^2) | O(n^2) | O(1) |
| Bucket Sort | Array | O(n+k) | O(n+k) | O(n^2) | O(nk) |
| Radix Sort | Array | O(nk) | O(nk) | O(nk) | O(n+k) |
Another crucial skill to master in the field of computer science is how to search for an item in a collection of data quickly. Here are the most common searching algorithms, their corresponding data structures, and time complexities.
Here are the main searching algorithms:
| Algorithm | Data Structure | Time Complexity - Average | Time Complexity - Worst | Space Complexity - Worst |
|---|---|---|---|---|
| Depth First Search | Graph of |V| vertices and |E| edges | - | O(|E|+|V|) | O(|V|) |
| Breadth First Search | Graph of |V| vertices and |E| edges | - | O(|E|+|V|) | O(|V|) |
| Binary Search | Sorted array of n elements | O(log(n)) | O(log(n)) | O(1) |
| Brute Force | Array | O(n) | O(n) | O(1) |
| Bellman-Ford | Graph of |V| vertices and |E| edges | O(|V||E|) | O(|V||E|) | O(|V|) |
Graphs are an integral part of computer science. Mastering them is necessary to become an accomplished software developer. Here is the data structure analysis of graphs:
| Node/Edge Management | Storage | Add Vertex | Add Edge | Remove Vertex | Remove Edge | Query |
|---|---|---|---|---|---|---|
| Adjacency List | O(|V|+|E|) | O(1) | O(1) | O(|V| + |E|) | O(|E|) | O(|V|) |
| Incidence List | O(|V|+|E|) | O(1) | O(1) | O(|E|) | O(|E|) | O(|E|) |
| Adjacency Matrix | O(|V|^2) | O(|V|^2) | O(1) | O(|V|^2) | O(1) | O(1) |
| Incidence Matrix | O(|V| ⋅ |E|) | O(|V| ⋅ |E|) | O(|V| ⋅ |E|) | O(|V| ⋅ |E|) | O(|V| ⋅ |E|) | O(|E|) |
Storing information in a way that is quick to retrieve, add, and search on, is a very important technique to master. Here is what you need to know about heap data structures:
Big Oh Notation Log
| Heaps | Heapify | Find Max | Extract Max | Increase Key | Insert | Delete | Merge |
|---|---|---|---|---|---|---|---|
| Sorted Linked List | - | O(1) | O(1) | O(n) | O(n) | O(1) | O(m+n) |
| Unsorted Linked List | - | O(n) | O(n) | O(1) | O(1) | O(1) | O(1) |
| Binary Heap | O(n) | O(1) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(m+n) |
| Binomial Heap | - | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) |
| Fibonacci Heap | - | O(1) | O(log(n))* | O(1)* | O(1) | O(log(n))* | O(1) |

Comments are closed.